위치 기반 동역학 (position-based dynamics) 코스 노트
27 Jan 2024Shape matching으로 대표되는 소프트 바디 시뮬레이션 방법을 여러 가지 용도로 잘 구현해서 써먹고 있었던 저는, 언제나 position-based dynamics도 관심이 있었습니다. 특히 unified paticle physics 라는 이름의 논문이 SIGGRAPH에서 선보여진 이후로는 언제나 그랬습니다. 고체, 액체, 기체 등등을 파티클 기반의 시뮬레이션으로 실시간에 그럴싸하게 만들 수 있다니, 그 자체로 매력적이죠 ㅎㅎ
언젠가 시간나면 좀 공부해봐야지 했었던 나날이 거의 10년이 된 시점인데, 시간이 남으면 보려고 했던 PBD의 코스 노트를 슬쩍슬쩍 번역해서 보려고 합니다.
위치 기반 동역학 코스 노트
원문: A Survey on Position Based Dynamics, 2017
저자
- 얀 벤더 (Jan Bender, RWTH Aachen University)
- 마티아스 뮐러 (Matthias Müller, NVIDIA PhysX Research)
- 마일스 맥클린 (Miles Macklin, NVIDIA PhysX Research)
그림 1: 위치 기반 동역학 프레임워크 내에서 시뮬레이션된 선택된 장면들
요약
기계적인 효과에 대한 물리 기반 시뮬레이션은 20여년 이상 컴퓨터 그래픽스의 중요한 연구 주제였습니다. 이 분야의 고전적인 방법은 뉴턴의 제 2법칙을 이산화하고 다양한 힘을 결정하여 변형 가능한 물체의 늘어남, 전단 (shearing), 굽힘, 혹은 유체의 압력 및 점도와 같은 다양한 효과를 시뮬레이션하는 것입니다. 이러한 힘이 주어졌을 때 속도, 그리고 최종적으로 위치는 가속도 결과의 수치 적분에 의해 결정됩니다.
지난 몇 년 동안 위치 기반 (position-based) 시뮬레이션 방법이 그래픽 커뮤니티에서 인기를 끌었습니다. 고전적인 시뮬레이션 접근 방식과 달리 이 방법은 준-정적 (quasi-static) 문제의 해를 기반으로 각 시뮬레이션 단계의 위치 변화를 직접 계산합니다. 따라서 위치 기반 접근 방식은 빠르고, 안정적이고, 제어가 가능하여 인터랙티브 환경에서 사용하기에 적합합니다. 이 방법은 일반적으로 힘 기반 (force-based) 방법만큼 정확하지는 않지만, 시각적으로 타당한 정도를 제공합니다. 따라서 위치 기반 시뮬레이션의 주요 응용 분야는 가상 현실, 컴퓨터 게임, 영화 및 광고의 특수 효과입니다.
이 튜토리얼에서는 먼저 위치 기반 동역학의 기본 개념을 소개합니다. 그런 다음 다양한 솔버를 제시하고 이를 준수 제약 (compliant constraint) 과 관련하여 암묵적 (implicit) 오일러 방법의 변형 공식과 비교합니다. 이러한 솔버의 수렴을 개선하기 위한 접근법을 논의합니다. 또한 탄성 막대, 천, 체적 변형체, 강체 시스템 및 유체를 시뮬레이션하기 위해 위치 기반 방법을 적용하는 방법을 보여줍니다. 또한 이방성 (anisotropy) 이나 가소성 (plasticity) 과 같은 복잡한 효과를 시뮬레이션하는 방법을 시연하고 성능을 개선하기 위한 접근 방식을 소개합니다. 마지막으로 전망을 제시하고 미해결 문제를 논의합니다.
- 키워드: physically-based animation, position-based dynamics, deformable solids, rigid bodies, fluids
- 카테고리 및 주제 설명자 (ACM CCS에 따름): Computer Graphics [I.3.7]: Three-Dimensional Graphics and Realism—Animation
튜토리얼 상세
발표자
얀 벤더 (Jan Vender) 얀 벤더는 2007년 초에 칼스루에 대학교에서 박사 학위를 받았습니다. 그의 논문 주제는 멀티바디 시스템의 인터랙티브 동역학 시뮬레이션이었습니다. 이후 칼스루에 공과대학에서 박사 후 연구원 (2007~2010년) 으로, 다름슈타트 공과대학교 계산공학 대학원 조교수 (2010~2016년) 로 물리 기반 시뮬레이션 분야에서 연구를 계속했습니다. 2016년부터는 아헨공과대학교 비주얼 컴퓨팅 연구소의 교수로 재직하며 컴퓨터 애니메이션 그룹을 이끌고 있습니다. 현재 연구 분야는 강체 동역학, 탈형성 (deformable) 고체, 유체, 위치 기반 방법, 충돌 감지 및 해결, 절단, 프랙처링, 실시간 시각화 등 다양합니다. 주요 그래픽스 컨퍼런스의 프로그램 위원회에서 활동했으며 IEEE 컴퓨터 그래픽스 및 응용 분야의 부편집장을 맡고 있습니다.
마티아스 뮐러 (Matthias Müller) 마티아스 뮐러는 1999년 취리히 연방 공과대학교에서 고밀도 고분자 시스템의 원자론적 시뮬레이션으로 박사 학위를 받았습니다. MIT 컴퓨터 그래픽스 그룹에서 박사후 과정(1999~2001년)을 거치면서 거시적 물리 기반 시뮬레이션으로 분야를 변경했습니다. 입자 기반 물 시뮬레이션 및 시각화, 유한 요소 기반 연성체, 천 시뮬레이션, 골절 시뮬레이션에 관한 논문을 발표했습니다. 그의 연구의 주요 초점은 컴퓨터 게임에서 사용할 수 있는 무조건 안정적이고 빠르며 제어 가능한 시뮬레이션 기법입니다. 이 튜토리얼과 가장 관련이 깊은 그는 위치 기반 시뮬레이션 기법 분야의 창시자 중 한 명입니다. 2002년에는 게임 미들웨어 회사인 노보덱스(2004년 AGEIA에 인수)를 공동 설립하여 연구 책임자로서 물리 시뮬레이션 라이브러리 PhysX의 혁신적인 새 기능 확장을 담당했습니다. 2008년 초에 AGEIA Technologies, Inc.를 인수한 이후 NVIDIA의 PhysX 연구팀장으로 재직하고 있습니다.
마일스 맥클린 (Miles Macklin) 마일스 맥클린은 NVIDIA의 PhysX 연구팀의 연구원입니다. 2013년부터 위치 기반 역학을 사용하여 구축된 NVIDIA Flex라는 통합 물리 라이브러리를 개발하고 있습니다. 플렉스의 기술은 SIGGRAPH에서 두 편의 논문을 발표했으며, 현재 여러 게임 및 시각 효과 스튜디오에 배포되었습니다. NVIDIA에 입사하기 전에는 소니 컴퓨터 엔터테인먼트에서 초기 플레이스테이션3 개발, 런던의 락스테디 스튜디오에서 배트맨 아캄 시리즈, 샌프란시스코의 루카스아트에서 스타워즈 프랜차이즈의 시각 효과 엔지니어로 게임 업계에서 일했습니다. 현재 그는 GPU를 이용한 실시간 시뮬레이션 및 렌더링 방법에 대해 연구하고 있습니다.
필요한 배경
이 튜토리얼에서는 물리 기반 애니메이션의 기초에 대해 간략한 소개를 하지만, 이 분야에 대한 일반적인 지식이 있으면 좋습니다.
잠재적 대상 고객
이 튜토리얼은 인터랙티브 물리 기반 시뮬레이션 방법에 관심이 있는 컴퓨터 애니메이션 분야의 연구자 및 개발자를 대상으로 합니다. 이 튜토리얼은 중급 수준의 튜토리얼입니다.
서론
강체, 연체 또는 천과 같은 솔리드 오브젝트의 시뮬레이션은 30년 이상 컴퓨터 그래픽스 분야에서 중요하고 활발한 연구 주제였습니다. 이 분야는 80년대 후반 Terzopoulos와 그의 동료들에 의해 그래픽스 분야에 소개되었습니다 [TPBF87a]. 그 이후로 많은 연구가 발표되었고 그 수는 빠르게 증가하고 있습니다. 이러한 발전을 문서화한 다양한 서베이 논문 [GM97, MTV05, NMK* 06, MSJT08, BET14] 이 존재합니다.
이 튜토리얼에서는 특별한 종류의 시뮬레이션 기법, 즉 위치 기반 접근법 [BMO*14] 에 초점을 맞춥니다. 이러한 방법은 원래 고체 시뮬레이션을 위해 개발되었습니다. 그러나 최근의 일부 연구에서는 위치 기반의 컨셉이 유체 및 관절 강체를 시뮬레이션하는 데에도 사용될 수 있음을 보여주었습니다. 고전적인 동역학 시뮬레이션 방법은 시스템의 운동량 변화를 적용된 힘에 대한 함수로 공식화하고 가속도 및 위치의 수치 적분을 통해 위치를 계산해 나갑니다. 반면 위치 기반 접근 방식은 준-정적 (quasi-static) 문제에 대한 해를 기반으로 위치를 직접 계산합니다.
물리 시뮬레이션은 계산 과학 (computational science) 분야에서 잘 연구된 문제여서, 유한 요소법 (Finite Element Method, FEM) [OH99], 유한 차분법 (Finite Differences Method) [TPBF87b], 유한 체적법 (Finite Volume Method) [TBHF03], 경계 요소법 (Boundary Element Method) [JP99], 혹은 입자 기반 (particle-based) 접근법 [DSB99, THMG04] 과 같이 잘 정립된 많은 방법이 그래픽스 분야에 채택되었습니다. 계산 물리학 및 화학에서 컴퓨터 시뮬레이션의 주요 목표는 실제 실험을 대체하여 가능한 한 정확도를 높이는 것입니다. 반면, 컴퓨터 그래픽스에서 물리 기반 시뮬레이션 방법의 주요 응용 분야는 영화와 광고의 특수 효과, 그리고 최근에는 컴퓨터 게임과 기타 인터랙티브 시스템입니다. 이 분야에서는 속도와 제어 가능성이 가장 중요한 요소이며 정확성 측면에서 요구되는 것은 시각적 개연성뿐입니다. 이는 실시간 애플리케이션에서 특히 그렇습니다.
위치 기반 방식은 특히 인터랙티브 환경에서 사용하기에 적합합니다. 높은 수준의 제어 기능을 제공하며 간단하고 빠른 명시적 시간 통합 방식을 사용하는 경우에도 안정적입니다. 이러한 접근 방식은 단순성, 견고성, 속도 덕분에 최근 컴퓨터 그래픽과 게임 업계에서 큰 인기를 끌고 있습니다.
충돌 감지는 모든 시뮬레이션 시스템에서 중요한 부분입니다. 그러나 이 주제에 대한 적절한 논의는 이 튜토리얼의 범위를 벗어납니다. 따라서 린과 고츠초크의 연구 [LG98] 와 테쉬너 외의 연구 [TKH*05] 를 참고하시기 바랍니다.
배경
컴퓨터 그래픽스에서 동역학 시스템을 시뮬레이션하는 데 가장 많이 사용되는 접근 방식은 힘 기반입니다. 내부 및 외부의 힘을 축적하여 뉴턴의 운동 제 2 법칙에 따라 가속도를 계산합니다. 그런 다음 시간에 대한 적분 방법을 사용하여 속도와 최종적으로 물체의 위치를 업데이트합니다. 몇몇 시뮬레이션 방법 (대부분 강체 시뮬레이터지만) 은 충격량 (impulse) 기반 동역학을 사용하고 속도를 직접 수정합니다 [BFS05, Ben07]. 이와 대조적으로, 기하 기반 (geometry based) 방법은 속도 레이어도 생략하고 즉시 위치값을 수정합니다. 위치 기반 접근법의 가장 큰 장점은 제어 가능성입니다. 힘 기반 시스템에서 명시적 적분 기법 (explicit integration scheme) 의 오버슈팅 문제를 피할 수 있습니다. 또한 충돌 제약 (collision constraint) 을 쉽게 처리할 수 있고 포인트를 유효한 위치에 프로젝션 시킴으로써 관통 (penetration) 문제를 완전히 해결할 수 있습니다.
힘 기반 접근 방식 중 가장 간단한 방법 중 하나는 질량-스프링 (mass-spring) 네트워크로 고체를 표현하고 시뮬레이션하는 것입니다. 질량-스프링 시스템은 스프링으로 연결된 점 질량 집합으로 구성됩니다. 이러한 시스템의 물리학은 간단하며 시뮬레이터도 쉽게 구현할 수 있습니다. 그러나 이 간단한 방법에는 몇 가지 중요한 단점이 있습니다.
- 물체의 동작은 스프링 네트워크가 설정된 방식에 따라 달라집니다.
- 원하는 동작을 얻기 위해 스프링 상수를 조정하는 것이 어려울 수 있습니다.
- 질량 스프링 네트워크는 체적 보존 (volume preservation) 이나 체적 반전 (volume inversion) 방지와 같은 체적 관련 현상을 직접적으로 포착할 수 없습니다.
유한 요소법은 고체를 유한한 수의 점 질량으로 대체하는 대신 전체 부피를 고려하기 때문에 위의 모든 문제를 해결합니다. 여기서 오브젝트는 볼륨을 유한한 크기의 여러 요소로 분할하여 이산화됩니다. 이러한 이산화는 질량-스프링 접근법에서와 같이 정점이 질점의 역할을 하고 요소 (보통 사면체) 가 여러 질점에 동시에 작용하는 일반화된 스프링으로 생각할 수 있는 메시를 생성합니다. 두 경우 모두 질점 또는 메시 정점에 적용되는 힘은 정점의 속도와 메시의 실제 변형으로 인해 계산됩니다.
이 튜토리얼에서는 속도 및 가속도 레이어를 생략하고 위치를 직접 수정하는 위치 기반 시뮬레이션 방법에 중점을 둡니다. 여기서는 먼저 물리 기반 시뮬레이션의 기본 사항을 소개한 후 다음 섹션에서 위치 기반 개념을 설명합니다.
운동 방정식
각 입자 $i$는 질량 $m_i$, 위치 $\mathbf{x}_i$, 그리고 속도 $\mathbf{v}_i$ 이렇게 세 개의 속성을 가지고 있습니다. 입자의 운동 방정식은 뉴턴의 제 2 법칙으로부터 유도됩니다:
%%% \begin{equation} \dot{\mathbf{v}}_i = \frac{1}{m_i} \mathbf{f}_i \end{equation} %%%
이때 $\mathbf{f}_i$는 입자 $i$에 적용되는 모든 힘의 합입니다. $\dot{\mathbf{x}}$와 $\mathbf{v}$의 관계는 속도 운동학 관계로 설명할 수 있습니다:
%%% \begin{equation} \dot{\mathbf{x}}_i = \mathbf{v} \end{equation} %%%
입자가 오직 세 개의 평행 이동 자유도만 가지고 있는 반면, 강체는 세 개의 회전 자유도 또한 가지고 있습니다. 따라서, 강체는 관성 텐서 $\mathbf{I}_i \in \mathbb{R}^{3 \times 3}$, 일반적으로 단위 쿼터니온 $\mathbf{q}_i \in \mathbb{H}$로 나타내는 회전 방향, 그리고 각속도 $\mathbf{\omega}_i \in \mathbb{R}^3$ 같은 추가적인 속성이 필요합니다. 강체의 경우 일반적으로 원점이 질량 중심에 있고 관성 텐서가 지역 좌표계에서 대각 행렬이 되게끔 축의 방향을 회전시킨 지역 좌표계가 선택됩니다.
뉴턴의 제2법칙은 실제로 입자에만 적용됩니다. 오일러는 강체를 무한한 수의 입자의 집합으로 간주하여 이 법칙을 강체의 경우로 확장했습니다. 따라서 강체에 대한 운동 방정식은 뉴턴-오일러 방정식이라고도 합니다. 강체의 회전 부분에 대한 운동 방정식은 다음과 같습니다:
%%% \begin{equation} \dot{\mathbf{\omega}}_i = \mathbf{I}_i^{-1} \left( \mathbf{\tau}_i - \left( \mathbf{\omega}_i \times \left( \mathbf{I}_i \mathbf{\omega}_i \right) \right) \right) \end{equation} %%%
이때 $\mathbf{\tau}_i$는 모든 모멘트의 합입니다. 모멘트는 순수 모멘트일수도 있고, 혹은 힘 $\mathbf{f}$가 점 $\mathbf{p}$에 작용하고 $\mathbf{x}$가 질량 중심일 때 힘 $\mathbf{t}=\left(\mathbf{p} - \mathbf{x}\right) \times \mathbf{f}$의 부산물일수도 있습니다. 회전부의 속도 운동학 관계는 다음과 같이 정의됩니다:
%%% \begin{equation} \dot{\mathbf{\omega}}_i = \frac{1}{2} \tilde{\mathbf{\omega}}_i \mathbf{q}_i \end{equation} %%%
이때 $\tilde{\mathbf{\omega}}_i$는 쿼터니온 $\left[ 0, \omega^x_i, \omega^y_i, \omega^z_i \right]$ 입니다.
시간 적분
제약이 없는 입자 또는 강체에 대한 시뮬레이션 단계는 각각 방정식 (1)-(2) 또는 방정식 (1)-(4)의 수치 적분에 의해 수행됩니다. 위치 기반 동역학 분야에서 가장 널리 사용되는 적분법은 다음에서 소개하는 심플렉틱 오일러 (symplectic Euler) 방법입니다.
잘 알려진 명시적 오일러 (explicit Euler) 방법와 달리 심플렉틱 오일러는 위치 벡터를 적분할 때 시간 $t_0$ 대신 시간 $t_0 + \Delta t$에서의 속도를 사용합니다. 그러면 입자에 대한 시간 적분은 다음 방정식에 의해 수행됩니다:
%%% \mathbf{v}_i \left( t_0 + \Delta t \right) = \mathbf{v}_i \left( t_0 \right) + \Delta t \frac{1}{m_i} \mathbf{f}_i\left( t_0 \right) %%%
%%% \mathbf{x}_i \left( t_0 + \Delta t \right) = \mathbf{x}_i \left( t_0 \right) + \Delta t \mathbf{v}_i \left( t_0 + \Delta t \right) %%%
강체의 경우 방정식 (3)과 (4) 또한 적분되어야 합니다. 심플렉틱 오일러 방법을 사용하면 다음과 같은 결과를 얻을 수 있습니다:
%%% \mathbf{\omega}_i \left( t_0 + \Delta t \right) = \mathbf{\omega}_i \left( t_0 \right) + \Delta t \mathbf{I}^{-1}_i \left( t_0 \right) \cdot \left( \mathbf{\tau}_i\left( t_0 \right) - \left( \mathbf{\omega}_i \left( t_0 \right) \times \left( \mathbf{I}_i \left( t_0 \right) \mathbf{\omega}_i \left( t_0 \right) \right) \right) \right) %%%
%%% \mathbf{q}_i \left( t_0 + \Delta t \right) = \mathbf{q}_i \left( t_0 \right) + \Delta t \frac{1}{2} \tilde{\mathbf{\omega}}_i \left( t_0 + \Delta t \right) \mathbf{q}_i \left( t_0 \right) %%%
수치 오류 때문에 쿼터니온이 회전을 나타내기 위해 만족해야하는 조건 $\left| \mathbf{q} \right| = 1$이 적분 이후 위반될 수 있음을 주의하세요. 따라서 쿼터니온 값은 매 시간 적분 단계 후에 정규화 되어야 합니다.
심플렉틱 오일러는 1차 적분기 (first-order integrator) 이며 알고리즘의 예측 단계에만 사용됩니다. 위치 기반 동역학 (Position Based Dynamics, PBD) 에서는 뒤의 “암묵적 방법과의 연결”절에 설명할 것처럼 구속력 (constraint force) 이 암묵적으로 적분됩니다.
제약 (constraint)
제약 조건은 물체의 상대적인 움직임을 제한하는 등식 및 부등식 형태의 운동학적 제한입니다. 등식 제약과 부등식 제약은 각각 양방향 (bilateral) 제약과 일방향 (unilateral) 제약이라고 합니다. 일반적으로 제약은 위치 및 회전 방향 변수, 선형 및 각속도, 그리고 모든 차수의 도함수에 대한 함수입니다. 그러나 위치 기반 시뮬레이션 방법은 위치에 의존적인 제약, 강체의 경우에는 여기에 추가로 회전 방향에 의존적인 제약까지만 고려합니다. 따라서 양방향 제약은 다음과 같은 함수로 정의됩니다:
%%%
C \left(
\mathbf{x}_{i_1},
\mathbf{q}_{i_1},
\ldots,
\mathbf{x}_{i_{n_j}},
\mathbf{q}_{i_{n_j}}
\right) = 0
%%%
그리고 일방향 제약은 다음과 같습니다:
%%%
C \left(
\mathbf{x}_{i_1},
\mathbf{q}_{i_1},
\ldots,
\mathbf{x}_{i_{n_j}},
\mathbf{q}_{i_{n_j}}
\right) \ge 0
%%%
여기서 $\left\{ i_1, \ldots, i_{n_j} \right\}$는 물체 인덱스의 집합이고 $n_j$는 제약의 카디널리티입니다. 일반적으로 PBD에서 사용되는 제약은 위치와 시간에만 의존적이고 속도에는 의존적이지 않습니다. 이러한 제약을 홀로노믹 (holonomic) 이라고 합니다.
제약은 운동학적 제한이므로 동역학에도 영향을 미칩니다. 고전적인 방법은 제약이 있는 동역학 시스템을 시뮬레이션하기 위해서 힘을 결정합니다. 예를 들어, 위치 에너지 $E = \frac{k}{2} C^2$를 정의하고 힘을 $f = - \nabla E$로 유도하거나 (soft constraint), 제약 동역학으로부터 유도된 라그랑주 승수를 통해 (hard constraint) 이를 수행합니다 [Wit97]. 이와 달리 위치 기반 접근법은 모든 제약들을 충족하기 위해 물체의 위치와 회전 방향을 직접 수정합니다.
위치 기반 동역학의 핵심
이번 절에서는 속도 및 가속도 레이어를 생략하고 위치에서 바로 작동하는 접근 방식인 위치 기반 동역학 (PBD) 를 소개합니다 [MHHR07]. 알고리즘을 설명하겠습니다. 그런 다음 시뮬레이션할 물체를 설명하는 제약 시스템을 푸는 방법에 대해 구체적으로 설명하겠습니다.
다음에서는 입자 시스템에 대한 위치 기반 접근 방식을 먼저 소개합니다. 강체를 처리하기 위한 확장은 “강체 동역학”절에서 설명합니다.
알고리즘
시뮬레이션할 오브젝트는 N개의 입자 집합과 M개의 제약 집합으로 표현됩니다. 각 제약에 대해 0에서 1 사이의 범위에서 제약의 강도를 정의하는 강성 (stiffness) 매개변수 k를 도입합니다. 이를 통해 사용자는 물체의 탄성을 더 세밀하게 제어할 수 있습니다.
시간 적분
이 데이터와 타임 스텝 $\Delta t$가 주어지면 알고리즘 1에 설명된 대로 시뮬레이션이 진행됩니다. 이 알고리즘은 시간에 대한 2차 시스템을 시뮬레이션하기 때문에, 시뮬레이션 루프가 시작되기 전에 (1)-(3)에서 입자의 위치와 속도를 모두 지정해야 합니다. 라인 (5)-(6)은 속도와 위치에 대해 간단한 심플렉틱 오일러 적분 단계를 수행합니다. 새로운 위치값 $\mathbf{p}_i$는 원래 위치 변수에 직접 할당되지 않고 예측에만 사용됩니다. 충돌 제약과 같은 비영구적인 외부 제약 조건은 각 타임 스텝이 시작될 때마다 식 (7)에서 처음부터 생성됩니다. 여기서 원본 위치와 예측 위치는 연속 충돌 감지를 수행하기 위해 사용됩니다. 그런 다음 솔버 (8)-(10)가 예측된 위치가 $M_{Coll}$ 외부 제약과 $M$ 내부 제약 조건을 만족하도록 반복적으로 보정합니다. 마지막으로 보정된 위치 $\mathbf{p}_i$를 사용하여 위치와 속도를 업데이트합니다. 여기서는 위치와 함께 속도를 업데이트하는 것이 필수적입니다. 이 작업을 수행하지 않으면 시뮬레이션에서 2차 시스템의 올바른 동작이 생성되지 않습니다. 보시다시피, 여기서 사용된 적분 방식은 Verlet 방식과 매우 유사합니다. 또한 시뮬레이션할 객체를 설명하기 위해 일련의 제약 조건을 사용하는 Jos Stam의 Nucleus 솔버 [Sta09]와도 밀접한 관련이 있습니다. 가장 큰 차이점은 Nucleus는 위치가 아닌 속도에 대한 제약 조건을 푼다는 점입니다.
1: for all vertices $i$ do
2: initialize $x_i = x_i^0$, $v_i = v_i^0$, $w_i = 1 / m_i$
3: end for
4: loop
5: for all vertices $i$ do $v_i <- v_i + \Delta t w_i f_{ext} (x_i)$
6: for all vertices $i$ do $p_i <- x_i + \Delta t v_i$
7: for all vertices $i$ do getCollConstraints($x_i -> p_i$)
8: loop $solverIteration$ times
9: projectConstraints(C_1, ..., C_{M+M_{Coll}}, p_1, ..., p_N)
10: end loop
11: for all vertices $i$ do
12: $v_i <- (p_i - x_i) / \Delta t$
13: $x_i <- p_i$
14: end for
15: velocityUpdate(v_1, ..., v_N)
16: end loop
알고리즘 1: 위치 기반 동역학
감쇠 (damping)
일반적으로 동역학 시뮬레이션의 품질은 적절한 감쇠 체계와의 통합으로 개선할 수 있습니다. 긍정적인 효과로 감쇠은 물체의 점 위치의 시간적 진동을 줄여 안정성을 향상시킬 수 있습니다. 이를 통해 더 큰 타임 스텝을 사용할 수 있으므로 동역학 시뮬레이션의 성능이 향상됩니다. 반면에 감쇠은 시뮬레이션된 물체의 동적인 움직임을 변경합니다. 그 결과 원하는 효과(예: 변형 가능한 고체의 진동 감소)를 얻거나 물체 전체의 선운동량 또는 각운동량 변화와 같은 교란 효과를 얻을 수 있습니다.
일반적으로 감쇠 항 $\mathbf{C}\dot{\mathbf{X}}$는 물체의 운동 방정식에 통합될 수 있는데, 여기서 $\dot{\mathbf{X}}$는 위치의 모든 1차 도함수의 벡터를 나타냅니다. 사용자 정의 행렬 C가 대각 행렬인 경우 점의 절대 속도가 감쇠되며, 이를 점 감쇠 (point damping) 라고도 합니다. 이러한 점 감쇠력을 적절히 계산하면 점의 가속도가 감소하여 수치 안정성이 향상됩니다. 이러한 특성은 마찰과 같은 일부 설정에서는 바람직합니다. 그러나 일반적인 경우 점 감쇠력으로 인한 물체의 전반적인 감속은 바람직하지 않습니다. 점 감쇠력은 예를 들어 [TF88] 또는 [PB88]에서 점 대 못과 같은 기하적 제약이 있는 동역학 시뮬레이션에 점 감쇠력을 사용하는 데 사용됩니다.
변형 가능한 물체의 선운동량 및 각운동량을 보존하기 위해서는 일반적으로 스프링 감쇠력이라고 하는 대칭 감쇠력을 사용할 수 있습니다. 이러한 힘은 행렬 $\mathbf{C}$에서 대각선 부분이 아닌 항목으로 나타낼 수 있습니다. 감쇠력은 예를 들어 Baraff와 Witkin [BW98] 또는 Nealen 외 [NMK*06]에 의해 설명됩니다. 이러한 힘은 위치 기반 방법에도 적용될 수 있습니다. 하지만 Baraff와 Witkin, Nealen 등의 접근 방식은 물체의 지오메트리의 토폴로지 정보에 의존하기 때문에 쉐입 매칭과 같은 메시리스 (meshless) 기법에는 적용할 수 없습니다.
점 및 스프링 감쇠을 사용하면 현재 속도 또는 상대 속도를 줄일 수 있습니다. 그러나 일반적으로 다음 타임 스텝에서의 예측 속도 또는 상대 속도를 고려하는 것이 더 적절합니다.
감쇠에서의 흥미로운 대안이 [SGT09]에서 제시되었습니다. 여기서는 대칭적이고 운동량을 보존하는 힘의 개념을 메시리스 표현으로 확장했습니다. 전역적인 대칭 감쇠력이 물체의 질량 중심을 기준으로 계산됩니다. 이러한 힘은 선운동량을 보존하는 반면, 각운동량의 보존은 상대 위치에 힘을 프로젝션하거나 선형 프로그래밍을 사용하여 토크를 제거함으로써 보장됩니다. [SGT09]에 제시된 접근 방식은 감쇠력을 반복적으로 계산합니다. 그러나 이 논문은 반복 프로세스의 수렴과 반복을 수행하지 않고도 솔루션을 직접 계산할 수 있는 방법도 보여줍니다. 따라서 이 접근법은 연결 정보 유무에 관계없이 임의의 위치 기반 변형 모델에 대한 감쇠력을 계산하는 효율적인 대안이 될 수 있습니다. 이 접근 방식은 사용자 정의 클러스터의 진동을 전역적으로 또는 지역적으로 감쇠하는 데 사용할 수 있습니다.
솔버
풀어야 하는 시스템
알고리즘 1에서 솔버 단계 (8)-(10)의 목표는 입자의 예측 위치가 모든 제약을 만족하도록 수정하는 것입니다. 이후 이 문서에서는 알고리즘 1과는 달리 솔버가 작동하는 입자의 위치에 대하여 위치를 나타내는 일반적인 기호인 $\mathbf{x}$를 사용할 것입니다. 알고리즘 1에는 더 큰 내용이 있으며 예측된 위치를 이전 타임 스텝에서의 위치와 구분하기 위해 기호 $\mathbf{p}$를 사용했습니다.
풀어야 하는 문제는 $3N$개의 모르는 위치값 성분에 대한 $M$개의 방정식 집합으로 구성되며, 여기서 이제 $M$은 제약의 총 개수입니다. 이 시스템은 대칭일 필요는 없습니다. $M > 3N (M < 3N)$ 이면 시스템이 과도 (과소) 결정된 것입니다. 비대칭성에 더하여 이 방정식은 일반적으로 비선형입니다. 간단한 거리 제약인 $C \left(\mathbf{x}_1, \mathbf{x}_2\right) = \left| \mathbf{x}_1 - \mathbf{x}_2 \right|^2 - d^2$ 함수는 비선형 방정식을 만들어 냅니다. 상황을 더욱 복잡하게 만드는 것은, 충돌이 등식이 아니라 부등식을 만들어 낸다는 사실입니다. 등식과 부등식이 있는 비대칭 비선형 시스템을 푸는 것은 어려운 문제입니다.
$\mathbf{x}$가 $\left[ \mathbf{x}_1^T, \ldots, \mathbf{x}_N^T \right]^T$와 같이 위치 벡터들을 합친 벡터이고 제약 함수 $C_j$가 합쳐진 벡터 $\mathbf{x}$를 입력받아 정의된 위치 좌표값 중 일부만 사용한다고 합시다. 그러면 풀어야 할 시스템은 다음과 같이 쓸 수 있습니다:
%%% C_1 \left( \mathbf{x} \right) \succ 0 %%%
%%% \ldots %%%
%%% C_M \left( \mathbf{x} \right) \succ 0 %%%
여기서 $\succ$은 $=$ 혹은 $\ge$를 뜻합니다. 뉴턴-랩슨 반복법은 등식만 있는 비선형 대칭 시스템만 푸는 방법입니다. 그 과정은 솔루션의 첫번째 추측값으로 시작합니다. 그다음 각 제약 함수는 다음 식을 이용하여 현재 솔루션에 대한 이웃 형태로 선형화됩니다:
%%% C \left( \mathbf{x} + \Delta \mathbf{x} \right) = C \left( \mathbf{x} \right) + \nabla C \left( \mathbf{x} \right) \cdot \Delta \mathbf{x} + O \left( \left| \Delta \mathbf{x} \right|^2 \right) = 0 %%%
이 식은 전역적인 수정 벡터 $\Delta \mathbf{x}$에 대한 선형 방정식을 만들어 냅니다:
%%% \nabla C_1 \left( \mathbf{x} \right) \cdot \Delta \mathbf{x} = -C_1 \left( \mathbf{x} \right) %%%
%%% \ldots %%%
%%% \nabla C_M \left( \mathbf{x} \right) \cdot \Delta \mathbf{x} = -C_M \left( \mathbf{x} \right) %%%
여기서 $\nabla C_j \left( \mathbf{x} \right)$는 제약 함수 $C_j$를 자신의 모든 매개변수에 대해 미분한 항을 담고 있는 $1 \times N$ 차원의 벡터이고, 여기서 $N$은 제약 함수와 관련된 $\mathbf{x}$ 안의 요소 개수입니다. 이는 또한 선형 시스템의 $j$번째 행이기도 합니다. 행렬의 행 $\nabla C_j \left( \mathbf{x} \right)$와 우변의 스칼라값 $-C_j \left( \mathbf{x} \right)$ 둘다 상수인데, 이는 이 시스템을 풀기 전에 위치 $\mathbf{x}$에서 평가되었기 때문입니다. $M = 3N$ 이고 등식만 주어지면, 이 시스템은 예를 들어 preconditioned conjugate gradient method 같은 아무 선형 솔버나 써도 풀 수 있습니다. $\Delta \mathbf{x}$에 대해 풀리면 현재 솔루션은 $\mathbf{x} \leftarrow \mathbf{x} + \Delta \mathbf{x}$로 업데이트 됩니다. 이 과정을 반복하면서 이후 새로운 위치에서의 $\nabla C_j \left( \mathbf{x} \right)$와 $-C_j \left( \mathbf{x} \right)$를 평가하여 새로운 선형 시스템을 생성합니다.
만약 $M \ne 3N$이라면 만들어진 선형 시스템 행렬은 비대칭이고 역행렬을 구할 수 없습니다. Goldenthal 등 [GHF*07]은 최소 자승의 개념에서 최상의 솔루션을 만들어 내는 시스템 행렬에 대한 의사 역행렬을 사용하여 이 문제를 해결합니다. 여전히 부등식 제약은 직접적으로 다루는 것이 불가능합니다.
비선형 가우스-자이델 (Gauss-Seidel) 솔버
PBD 접근법에서는 비선형 가우스-자이델 방법이 사용됩니다. 이 방법은 각 제약 방정식을 따로 풀어냅니다. 각 제약은 연관된 모든 입자 위치에 대한 하나의 스칼라 방정식 $C \left( \mathbf{x} \right) \succ 0$을 만들어 냅니다. 따라서 이 서브시스템은 매우 과소 결정되어 있습니다. PBD는 이를 다음과 같이 풀어냅니다. 다시 한번, $\mathbf{x}$가 주어졌을 때 $C \left( \mathbf{x} + \Delta \mathbf{x} \right) \succ 0$를 만족하는 보정 벡터 $\Delta \mathbf{x}$를 찾고자 합니다. PBD 또한 제약 함수를 선형화하지만 각 제약을 개별적으로 합니다. 제약 방정식은 다음과 같이 근사화됩니다:
%%% \begin{equation} C \left( \mathbf{x} + \Delta \mathbf{x} \right) = C \left( \mathbf{x} \right) + \nabla C \left( \mathbf{x} \right) \cdot \Delta \mathbf{x} \succ 0 \end{equation} %%%
시스템이 과소 결정되는 문제는 $\Delta \mathbf{x}$를 $\nabla C \left( \mathbf{x} \right)$의 방향에 있도록 제한함으로써 해결되는데, 이는 선운동량 및 각운동량을 보존하는 데에도 필요합니다. 이는 다음과 같은 보정 벡터로 위 방정식을 푸는데 단 하나의 스칼라 라그랑지안 승수 $\lambda$를 찾아야 한다는 의미입니다:
%%% \begin{equation} \Delta \mathbf{x} = \lambda \mathbf{X}^{-1} \nabla C \left( \mathbf{x} \right)^T \end{equation} %%%
여기서 $\mathbf{M} = diag \left( m_1, m_2, \ldots, m_N \right)$입니다. 이는 단일 입자 $i$의 보정 벡터에 대하여 다음과 같은 공식을 만들어 냅니다:
%%% \begin{equation} \Delta \mathbf{x}_i = - \lambda w_i \nabla_{\mathbf{x}_i} C \left( \mathbf{x} \right)^T \end{equation} %%%
여기서 $\lambda$는 다음과 같으며:
%%% \begin{equation} \lambda = \frac{C \left( \mathbf{x} \right)} {\sum_j w_j \left| \nabla_{\mathbf{x}_j} C \left( \mathbf{x} \right) \right|^2} \end{equation} %%%
$w_i = \frac{1}{m_i}$입니다. 모든 위치를 붙인 벡터 $\mathbf{x}$에 대해 수식화하면 다음 식을 얻습니다:
%%% \begin{equation} \lambda = \frac{C \left( \mathbf{x} \right)} {\nabla C \left( \mathbf{x} \right) \mathbf{M}^{-1} \nabla C \left( \mathbf{x} \right)^T} \end{equation} %%%
앞서 설명한 바와 같이 이 솔버는 제약 함수들을 선형화합니다. 하지만 뉴턴-랩슨 방법과는 달리 선형화가 각 제약마다 개별적으로 일어납니다. 선형화가 각 거리 제약의 프로젝션에 영향을 주지 않는다는 점은 중요한 사항입니다. 전체적으로는 비선형일지라도 하나의 거리 제약은 탐색 방향 위에서 일어나는 제약 그라디언트 상에서 선형이기 때문입니다. 이는 ‘사면체 메시’ 절에서 살펴보게 될 사면체 부피 제약 같은 다른 제약에 대해서도 마찬가지로 참입니다. 이러한 종류의 제약은 한번의 스텝으로 해결될 수 있습니다. 제약이 처리된 후 위치가 즉각적으로 업데이트 되기 때문에, 이러한 업데이트는 다음 제약의 선형화에도 영향을 마치게 되는데 이는 선형화가 실제 위치에 의존적이기 때문입니다. 각 제약은 미지의 라그랑주 승수 $\lambda$에 대해 하나의 스칼라 방정식을 생성하기 때문에 비대칭은 문제가 되지 않습니다. 부등식도 $C \left( \mathbf{x} \right) \ge 0$ 인지 먼저 체크해봄으로써 자명하게 처리가 됩니다. 부등식을 만족한다면 해당 제약은 그냥 넘어가면 됩니다.
각 제약이 프로젝션 전에 개별적으로 선형화된다는 점은 뉴턴 반복의 전체 전역적 솔루션에 대해 선형화를 고정한 채로 유지시키는 전역적 접근법에 비해 솔버를 더 안정적으로 만들어 줍니다.
아직까지는 강성 매개변수 $k$에 대해 고려하지 않았습니다. 이를 도입하는 몇 가지 방법이 있습니다. 가장 간단한 방법은 보정 벡터 $\Delta \mathbf{x}$에 $k \in \left[ 0, \ldots, 1 \right]$을 곱하는 것입니다. 그러나 솔버가 여러 번 반복함에 따라서 $k$의 영향이 비선형적이 됩니다. $n_s$번의 솔버 반복 이후 단일 거리 제약에 남는 에러값은 $\Delta \mathbf{x} \left( 1 - k \right)^{n_s}$가 됩니다. 선형적인 관계를 만들기 위해서는 보정 벡터에 $k$를 직접 곱하지 않고 $k’ = 1 - \left(1 - k \right)^{n_s}$를 곱합니다. 이 변환을 통해서 에러는 $\Delta \mathbf{x} \left( 1 - k’ \right)^{n_s} = \Delta \mathbf{x} \left(1 - k \right)$가 되고, 따라서 목표로 하는 $n_s$에 상관없이 $k$와 선형적인 의존 관계가 됩니다. 하지만 결과적으로 만들어진 재질에 대한 강성도는 여전히 시뮬레이션 타임 스텝에 대해 의존적입니다. 실시간 환경에서는 통상적으로 고정된 타임 스텝을 사용하므로 이러한 의존성은 큰 문제가 되지 않습니다.
계층적 (hierarchical) 솔버
가우스-자이델 방법은 안정적으로 구현하기 쉽지만 통상적으로 전역 솔버에 비해 심각하게 느리게 수렴합니다. 주된 원인은 에러 보정이 한 제약에서 다른 제약으로 지역적으로 전파되기 때문입니다. 따라서 가우스-자이델 방법은 고주파 에러를 저주파 에러보다 훨씬 더 빠르게 안정시키기 때문에 스무서라고 부릅니다.
가우스-사이델 방법의 수렴 속도를 높이기 위해 널리 사용되는 방법은 거친 (coarse) 메시가 도메인 전체에 에러 수정을 빠르게 전파하도록 하는 메시 계층 구조를 만드는 것입니다. 스무더는 계층 구조의 모든 메시에서 하나씩 작동하며, 에러 수정은 일반적으로 세밀한 수준에서 거친 수준으로 그리고 다시 여러 주기로 서로 다른 해상도의 메시로 이월됩니다. 이 기법을 다중 그리드 (multi-grid) 방식[GW06]이라고 합니다. 거친 메시에서 세밀한 메시로, 세밀한 메시에서 거친 메시로 보정값을 전송하는 것을 각각 연장 (prolongation) 및 제한 (restriction) 이라고 합니다. 다중 그리드 방법은 계층 구조가 생성되는 방식, 제한 및 연장 연산자의 세분화 방법, 메시가 처리되는 순서에서 차이가 있습니다.
[Mül08]에서 뮐러 등은 이 기법을 사용하여 계층적 위치 기반 동역학(HPBD)을 소개했습니다. 이들은 최초 시뮬레이션 메시를 계층 구조의 가장 미세한 메시로 정의하고 이전 메시의 입자들의 하위 집합만 유지하는 방식으로 더 거친 메시를 생성합니다. 계층 구조는 가장 거친 수준에서 가장 미세한 수준으로 한 번만 순회합니다. 따라서 연장 연산자만 정의하면 됩니다. 특정 단계의 각 입자가 이전의 더 거친 단계의 입자 두 개 이상에 연결되도록 함으로써 (그림 2 참조), 연장은 더 거친 단계의 인접 입자로부터 정보를 보간하는 것과 같습니다. 또한 이들은 원래 메시의 제약을 기반으로 거친 메시에서 거리 제약을 생성하는 방법도 제안하였습니다. 이러한 거친 제약은 일방 (unilateral) 이어야 하며, 즉 현재 거리가 휴식 상태 거리보다 클 경우에만 작용해야 하며 그렇지 않으면 구부러짐이나 접힘을 방지할 수 있다는 점에 유의해야 합니다.
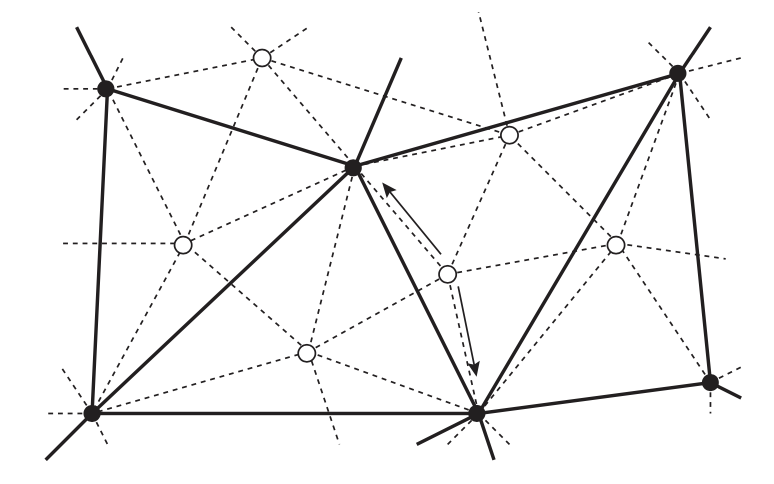그림 2: 메시 계층구조의 구성: 세밀한 레벨 $l$은 표시된 모든 입자와 점선으로 표시된 제약으로 구성됩니다.
그 다음 거친 레벨 $l + 1$에는 검은색 입자의 적절한 하위 집합과 실선 제약으로 구성되어 있습니다. 각 세밀한
흰색 입자는 화살표로 표시된 부모인 최소 $k ( = 2 )$ 개의 검은색 입자에 연결되어야 합니다.
암묵적 방법과의 연결
Liu 등[LBOK13]이 지적한 바와 같이, PBD는 암묵적 역방향 오일러 적분 방식과 밀접한 관련이 있습니다. 이는 역방향 오일러를 위치에 대한 제약이 있는 최소화라고 생각해 보면 알 수 있습니다. 운동 방정식의 전통적인 암묵적 오일러 시간 이산화부터 시작해 봅시다:
%%% \begin{equation} \mathbf{x}^{n+1} = \mathbf{x}^n + \Delta t \mathbf{v}^{n+1} \end{equation} %%%
%%% \begin{equation} \mathbf{v}^{n+1} = \mathbf{v}^n + \Delta t \mathbf{M}^{-1} \left( \mathbf{F}_{ext} + k \nabla \mathbf{C}^{n+1} \right) \end{equation} %%%
이때 $\mathbf{C}$는 제약 전위 벡터를, $k$는 강성 파라미터를 나타냅니다. 위 식에서 속도를 제거하면 다음을 얻습니다:
%%% \begin{equation} \mathbf{M} \left( \mathbf{x}^{n+1} - 2 \mathbf{x}^n + \mathbf{x}^{n-1} - \Delta t^2 \mathbf{M}^{-1} \mathbf{F}_{ext} \right) = \Delta t^2 k \nabla \mathbf{C}^{n+1} \end{equation} %%%
식 (12)는 다음 최적화 식의 1차 최적 조건으로 볼 수 있습니다:
%%% \begin{equation} \min_{\mathbf{x}} \frac{1}{2} \left( \mathbf{x}^{n+1} - \tilde{\mathbf{x}} \right)^T \mathbf{M} \left( \mathbf{x}^{n+1} - \tilde{\mathbf{x}} \right) - \Delta t^2 k \nabla \mathbf{C}^{n+1} \end{equation} %%%
여기서 $\tilde{\mathbf{x}}$는 예측된 위치값이며, 다음과 같이 주어집니다:
%%% \begin{equation} \tilde{\mathbf{x}} = 2 \mathbf{x}^n - \mathbf{x}^{n-1} + \Delta t^2 \mathbf{M}^{-1} \mathbf{F}_{ext} \end{equation} %%%
%%% \begin{equation} = \mathbf{x}^n + \Delta t \mathbf{v}^n + \Delta t^2 \mathbf{M}^{-1} \mathbf{F}_{ext} \end{equation} %%%
$k \rightarrow \infty$로 가는 극한을 취하면 다음과 같은 제약이 있는 최적화식을 얻을 수 있습니다:
%%% \begin{equation} \min_{\mathbf{x}} \frac{1}{2} \left( \mathbf{x}^{n+1} - \tilde{\mathbf{x}} \right)^T \mathbf{M} \left( \mathbf{x}^{n+1} - \tilde{\mathbf{x}} \right) \end{equation} %%%
%%% \textit{s.t.} \ C_i \left( \mathbf{x}^{n+1} \right) = 0, i = 1, \ldots, n. %%%
이 최소화 문제는 제약 다양체 상에서 예측된 위치 (질량 가중치 측정) 에 가장 가까운 점을 찾는 것으로 해석할 수 있습니다. PBD는 골드엔탈 외[GHF07]의 빠른 프로젝션 알고리즘의 변형을 사용해 이 최소화를 근사 해결하는데, 이 알고리즘은 먼저 예측 단계를 거친 다음 파티클을 제약 다양체에 반복적으로 프로젝션합니다. PBD는 이 접근법을 따르지만 프로젝션 단계를 푸는 데 사용되는 방법이 다릅니다. [GHF07]과 달리 PBD는 각 뉴턴 단계에서 시스템 전체를 선형화하여 풀지 않습니다. 대신 “풀어야 할 시스템”절에서 설명한 바와 같이 가우스-자이델 방식과 같이 한 번에 하나의 제약을 선형화합니다. 이는 큰 비선형성 제약이 있을 때 PBD를 견고하게 만드는 데 도움이 됩니다.
투영 역학 (projective dynamics) [BML*14]은 제약의 무한 강성에 의존하지 않는 암묵적 방식으로 제약을 처리할 수 있는 PBD의 수정 버전을 제시합니다. 이는 솔루션을 예측된 (관성) 위치로 끌어당기는 역할을 하는 제약을 추가함으로써 달성됩니다.
이차 방법 (second-order methods)
역방향 오일러 방법과의 연결이 설정되었으니 더 높은 차수의 적분 방식을 PBD에 적용할 수 있습니다. [EB08]의 도출에 따라서 2차 정확도의 다단계 방법인 BDF2를 차용하겠습니다. 먼저 2차 정확도의 BDF2 업데이트 방정식을 다음과 같이 작성합니다:
%%% \begin{equation} \mathbf{x}^{n+1} = \frac{4}{3} \mathbf{x}^{n} - \frac{1}{3} \mathbf{x}^{n-1} + \frac{2}{3} \Delta t \mathbf{v}^{n+1} \end{equation} %%%
%%% \begin{equation} \mathbf{v}^{n+1} = \frac{4}{3} \mathbf{v}^{n} - \frac{1}{3} \mathbf{v}^{n-1} + \frac{2}{3} \Delta t \mathbf{M}^{-1} \left( \mathbf{F}_{ext} + k \nabla \mathbf{C}^{n+1} \right) \end{equation} %%%
속도를 제거하고 식을 정리하면 아래와 같이 됩니다:
%%% \begin{equation} \mathbf{M} \left( \mathbf{x}^{n+1} - \tilde{\mathbf{x}} \right) = \frac{4}{9} \Delta t^2 k \nabla \mathbf{C}^{n+1} \end{equation} %%%
여기서 관성 위치 $\tilde{\mathbf{x}}$는 다음과 같이 주어집니다:
%%% \begin{equation} \tilde{\mathbf{x}} = \frac{4}{3} \mathbf{x}^{n} - \frac{1}{3} \mathbf{x}^{n-1} + \frac{8}{9} \Delta t \mathbf{v}^{n} - \frac{2}{9} \Delta t \mathbf{v}^{n-1} + \frac{4}{9} \Delta t^2 \mathbf{M}^{-1} \mathbf{F}_{ext} \end{equation} %%%
식 (19)는 (16)과 같은 형태의 최소화에 대한 최적 조건으로 생각할 수 있습니다. 제약들이 풀리고나면, 업데이트 되는 속도는 식 (17)을 통해 얻을 수 있습니다:
%%% \begin{equation} \mathbf{v}^{n+1} = \frac{1}{\Delta t} \left[ \frac{2}{3} \mathbf{x}^{n+1} - 2 \mathbf{x}^{n} + \frac{1}{2} \mathbf{x}^{n-1} \right] \end{equation} %%%
이쪽 방식이 보다 정확한지 평가하기 위해서는 이전의 위치와 속도만 추가적으로 저장하고 예측 및 속도 업데이트 단계에서 몇 가지 기본 산술을 추가로 수행하면 되며, 나머지 PBD 알고리즘은 변경되지 않습니다. 이 간단한 수정의 이점은 수치적 댐핑이 훨씬 줄어들고 제약 프로젝션에 대한 수렴이 빨라진다는 점입니다. 이는 알고리즘이 이전 타임 스텝 정보를 사용하여 제약 다양체에 더 가까운 예측 위치를 생성하여 프로젝션을 더 빠르게 만든다고 생각하면 이해할 수 있습니다.
XPBD
지금까지 설명한 PBD의 한계 중 하나는 제약 강성이 제약 솔버에서 사용하는 타임 스텝 크기와 반복 횟수에 따라 달라진다는 것입니다. 무한한 제약 반복의 한계에서는 제약이 무한히 강해집니다. 놀랍게도 이러한 무한 강성 솔루션으로의 수렴은 제약 강성 계수를 어떻게 설정하든 상관없이 발생합니다.
PBD의 타임 스텝 및 반복 횟수에 강성이 종속되는 문제는 XPBD[MMC16]라는 확장으로 해결되었습니다. XPBD는 각 제약에 역강성 (inverse stiffness), 혹은 적합성 (compliance) $\alpha = \frac{1}{k}$를 연관시키는 적합성 제약 공식[SLM06]으로부터 파생됩니다.
XPBD를 도출하면 PBD의 반복 중에 각 제약에 대하여 계산된 $\lambda$를 총 승수의 증분 변화로 생각할 수 있음을 알 수 있습니다. 이는 일반적인 PBD의 방정식 (9)를 다음과 같이 수정합니다.
%%% \begin{equation} \Delta \lambda = \frac{ -C \left( \mathbf{x} \right) - \tilde{\alpha} \lambda }{ \nabla C \left( \mathbf{x} \right) \mathbf{M}^{-1} \nabla C \left( \mathbf{x} \right)^T + \tilde{\alpha} } \end{equation} %%%
여기서 $\tilde{\alpha} = \frac{\alpha}{\Delta t^2}$은 타임 스텝으로 스케일된 적합성 파라미터입니다.
이제 각 반복 이후 다음과 같이 시스템 위치값 뿐만 아니라 각 제약의 전체 라그랑지안 승수값도 업데이트 합니다:
%%% \begin{equation} \lambda = \lambda + \Delta \lambda \end{equation} %%%
%%% \begin{equation} \mathbf{x} = \mathbf{x} + \Delta \mathbf{x} \end{equation} %%%
(22)의 분모에 있는 추가항은 어떤 제약이 적용할 수 있는 힘의 양을 제한하는 형태로 작용하는데, 특히 $\lambda$가 커질수록 증가하는 제약의 변화는 작아지게 됩니다. 제로 적합성 ($\alpha = 0$) 의 경우에는 무한 강성의 제약에 따르는 일반적인 PBD와 정확히 일치하는 식을 얻게 됩니다.
전체 라그랑지안 승수 $\lambda$에는 유용한 해석이 있습니다. 이것은 제약이 입자들에 적용하는 힘의 총량을 잰 것으로, 이는 햅틱 장비나 힘에 의존적인 효과를 드라이빙하는데 사용될 수 있는 물리적인 양입니다.
XPBD가 PBD를 더 빠르게 수렴시키지는 않고 강성 솔루션에 도달하기 위해 동일한 반복 횟수가 필요할 것임을 주의하세요.
XPBD를 사용한다고 PBD가 더 빨리 수렴하지는 않으며, 강성 솔루션에 도달하기 위해서는 동일한 수의 반복이 필요합니다. 하지만 XPBD는 잘 정의된 에너지 포텐셜과 상관 관계가 있는 일관된 솔루션을 반환합니다. PBD와 마찬가지로 수렴 전에 솔버가 종료되면 제약 조건을 인위적으로 준수하는 것으로 나타납니다.
특정 제약들
다음으로는 PBD로 관절이 있는 강체 (articulated rigid body), 연체 (soft body), 천 (cloth) 또는 유체 (fluid) 와 같은 다양한 물질을 시뮬레이션하는 데 사용할 수 있는 다양한 제약 조건을 소개합니다. 가독성을 높이기 위해 $\mathbf{x}_{i,j} = \mathbf{x}_{i} - \mathbf{x}_{j}$로 정의하겠습니다.
늘어남 (stretching)
예를 들어 거리 제약 함수 $C \left( \mathbf{x}_1, \mathbf{x}_2 \right) = \left| \mathbf{x}_{1,2} \right| - d$를 고려해 봅시다. 각 점에 대해 미분하면 $\mathbf{n} = \frac{\mathbf{x}_{1,2}}{\left| \mathbf{x}_{1,2} \right|}$일때 각각 $\nabla_{\mathbf{x}_1} C \left( \mathbf{x}_1, \mathbf{x}_2 \right) = \mathbf{n}$, $\nabla_{\mathbf{x}_2} C \left( \mathbf{x}_1, \mathbf{x}_2 \right) = - \mathbf{n}$입니다. 따라서 스케일링 팩터 $\lambda = \frac{\left| \mathbf{x}_{1,2} \right| - d}{1 + 1}$이고 최종 보정은 다음과 같습니다:
%%% \Delta \mathbf{x}_1 = - \frac{w_1}{w_1 + w_2} \left( \left| \mathbf{x}_{1,2} \right| - d \right) \mathbf{n} %%%
%%% \Delta \mathbf{x}_2 = + \frac{w_2}{w_1 + w_2} \left( \left| \mathbf{x}_{1,2} \right| - d \right) \mathbf{n} %%%
이는 [Jak01]에서 거리 제약의 투영에 대한 공식입니다 (그림 3을 참고하세요). 이것들은 일반적인 제약 프로젝션 방법의 특수한 경우로 파생될 수 있습니다.
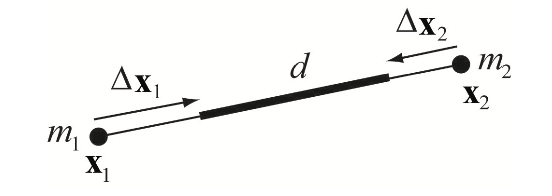그림 3: 제약 $C \left( \mathbf{x}_1, \mathbf{x}_2 \right) = \left| \mathbf{x}_{1,2} \right| - d$의
프로젝션. 보정 $\Delta \mathbf{x}_i$는 질량의 역수 $w_i = \frac{1}{m_i}$에 따라 가중치를 받습니다.
구부러짐 (bending)
천 시뮬레이션에서는 늘어남 저항 (resistance) 과 더불어서 구부러짐을 시뮬레이션하는 것이 중요합니다. 이를 위해 인접한 삼각형 $\left( \mathbf{x}_1, \mathbf{x}_3, \mathbf{x}_2 \right)$와 $\left( \mathbf{x}_1, \mathbf{x}_2, \mathbf{x}_4 \right)$ 한 쌍에 대하여 다음과 같은 제약 함수와 강성 $k_{bend}$를 사용하여 양방향 구부러짐 제약이 추가됩니다:
%%% C_{bend} \left( \mathbf{x}_1, \mathbf{x}_2, \mathbf{x}_3, \mathbf{x}_4 \right) = \textrm{acos} \left( \frac{\mathbf{x}_{2,1} \times \mathbf{x}_{3,1}}{ \left| \mathbf{x}_{2,1} \times \mathbf{x}_{3,1} \right|} \cdot \frac{\mathbf{x}_{2,1} \times \mathbf{x}_{4,1}}{ \left| \mathbf{x}_{2,1} \times \mathbf{x}_{4,1} \right|} \right) - \phi_0 %%%
스칼라 $\phi_0$는 초기 두 삼각형의 끼인각이고 $k_{bend}$는 천의 구부러짐 강도를 정의하는 전역 파라미터입니다 (그림 4를 참고하세요). 점 $\mathbf{x}_3$과 $\mathbf{x}_4$ 사이의 거리 제약에 더하여 이 구부러짐 항을 이용하는 것의 장점은 이 항이 늘어남과는 독립적이라는 것입니다. 이는 이 항이 에지의 길이와 독립적이기 때문입니다. 그림 5에서는 구부러짐과 늘어남을 독립적으로 튜닝하는 방식을 보여줍니다.
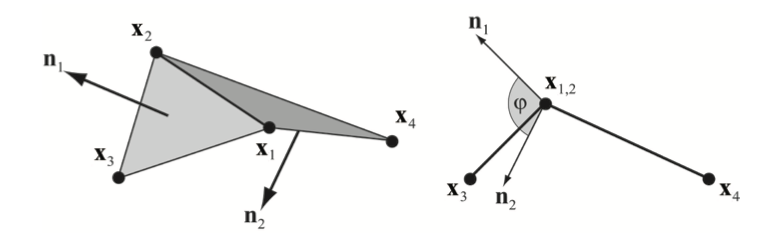그림 4: 구부러짐 저항에 대해서는 제약 함수
$C \left( \mathbf{x}_1, \mathbf{x}_2, \mathbf{x}_3, \mathbf{x}_4 \right) =
\textrm{arccos} \left( \mathbf{n}_1 \cdot \mathbf{n}_2 \right) - \phi_0$가 사용됩니다.
현재의 끼인각 $\phi$은 두 삼각형의 법선 사이의 각으로 측정됩니다.
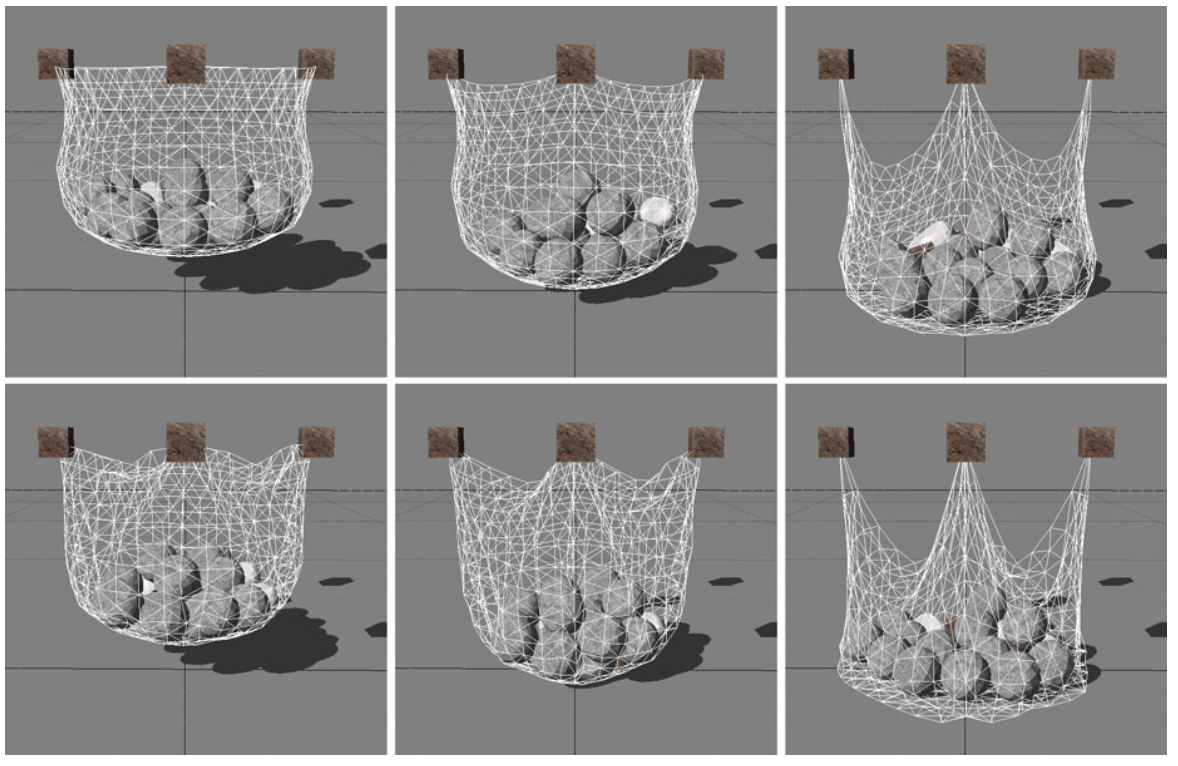그림 5: 이 그림은 늘어남 및 구부러짐 제약을 사용하여 시뮬레이션한 메시를 보여줍니다. 위쪽 행은 각각
$\left( k_\textrm{stretching}, k_\textrm{bending} \right) =
\left( 1, 1 \right), \left( \frac{1}{2}, 1 \right), \left( \frac{1}{100}, 1 \right)$인 경우를
보여줍니다. 아래쪽 행은 각각 $\left( k_\textrm{stretching}, k_\textrm{bending} \right) =
\left( 1, 0 \right), \left( \frac{1}{2}, 0 \right), \left( \frac{1}{100}, 0 \right)$인 경우입니다.
등척성 구부러짐 (isometric bending)
늘어나지 않는 면에 대한 구부러짐 제약은 [BKCW14]에서 소개되었습니다. 이 제약의 정의는 베르구 등[BWH∗06]의 이산화된 등척성 구부러짐 모델을 기반으로 하며, 표면이 등척적으로 변형되는 경우, 즉 에지의 길이가 변하지 않는 경우에 적용할 수 있습니다. 많은 직물들이 심하게 늘어날 수 없기 때문에, 이 방법은 의류 시뮬레이션에 적합한 선택입니다.
각 내부 에지 $e_i$에 대하여 스텐실 $s$는 $e_i$에 이웃하는 두 삼각형으로 구성된 것으로 정의됩니다. 벡터 $\mathbf{x}_s = \left( \mathbf{x}_0, \mathbf{x}_1, \mathbf{x}_2, \mathbf{x}_3 \right)^T$는 스텐실의 네 점을 담고 있고 벡터 $\mathbf{e}_s = \left[ \mathbf{x}_0\mathbf{x}_1, \mathbf{x}_1\mathbf{x}_2, \mathbf{x}_2\mathbf{x}_0, \mathbf{x}_0\mathbf{x}_3, \mathbf{x}_3\mathbf{x}_1 \right]$은 공유 에지로 시작하여 스텐실의 다섯 에지를 담고 있습니다 (그림 6을 참고하세요).
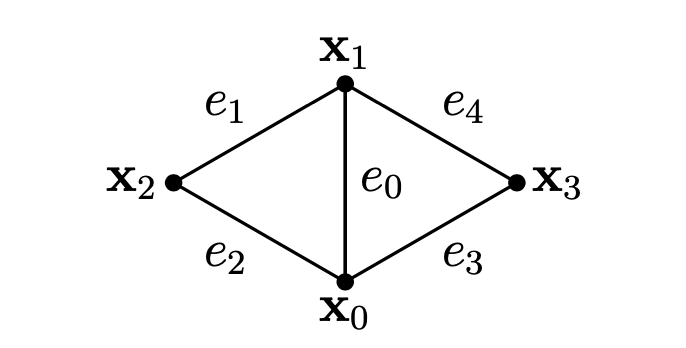그림 6: 등척성 구부러짐 제약은 내부 에지 $e_0$의 스텐실을 사용하여 정의됩니다.
등척성 구부러짐 모델을 사용하여 스텐실의 지역적 헤시안 구부러짐 에너지는 다음과 같이 결정됩니다:
%%% \mathbf{Q} = \frac{3}{A_0 + A_1} \mathbf{K}^T \mathbf{K} %%%
여기서 $A_0$와 $A_1$은 이웃하는 삼각형의 면적이고 $\mathbf{K}$는 다음과 같은 벡터입니다:
%%% \mathbf{K} = \left( c_{01} +c_{04}, c_{02} +c_{03}, −c_{01} −c_{02}, −c_{03} −c_{04} \right) %%%
여기서 $c_{jk} = \textrm{cot} \angle e_j, e_k$입니다. 행렬 $\mathbf{Q} \in \mathbb{R}^{4 \times 4}$는 상수이며 스텐실의 초기 구성으로부터 미리 계산할 수 있습니다. 지역적 헤시안 구부러짐 에너지는 구부러짐 제약을 정의하는데 다음과 같이 사용될 수 있습니다:
%%% C_{bend} \left( \mathbf{x}_s \right) = \frac{1}{2} \sum_{i,j} \mathbf{Q}_{i,j} \mathbf{x}_i^T\mathbf{x}_j %%%
헤시안 구부러짐 에너지가 상수이므로, 그라디언트는 다음과 같이 결정됩니다: %%% \frac{\partial C_{bend}}{\partial \mathbf{x}_i} = \sum_{j} \mathbf{Q}_{i,j} \mathbf{x}_j %%%
그림 7은 소개된 구부러짐 제약을 사용하여 시뮬레이션된 천을 보여줍니다.
그림 7: 무거운 구체가 네 동상 위로 던져진 천 조각을 내리누르고 있습니다. 등척성 구부러짐 제약 때문에 사실적인
주름이 만들어집니다.
충돌 (collision)
삼각형 충돌
천 내부의 자체 충돌 (self collision) 은 추가적인 일방향 (unilateral) 제약에 의해 처리할 수 있습니다. 삼각형 $\mathbf{x}_1, \mathbf{x}_2, \mathbf{x}_3$을 통과하여 움직이려는 점 $\mathbf{q}$에 대한 제약 함수는 다음과 같습니다:
%%% C \left( \mathbf{q}, \mathbf{x}_1, \mathbf{x}_2, \mathbf{x}_3 \right) = \left( \mathbf{q} - \mathbf{x}_1 \right) \cdot \frac{\mathbf{x}_{2,1} \times \mathbf{x}_{3,1}}{\left| \mathbf{x}_{2,1} \times \mathbf{x}_{3,1} \right|} - h %%%
여기서 $h$는 천의 두께입니다 (그림 8을 참고하세요). 만약 점이 삼각형 법선을 기준으로 아래에서부터 들어오는 경우 제약 함수는 다음과 같아야 합니다:
%%% C \left( \mathbf{q}, \mathbf{x}_1, \mathbf{x}_2, \mathbf{x}_3 \right) = \left( \mathbf{q} - \mathbf{x}_1 \right) \cdot \frac{\mathbf{x}_{3,1} \times \mathbf{x}_{2,1}}{\left| \mathbf{x}_{3,1} \times \mathbf{x}_{2,1} \right|} - h %%%
그림 8: 제약 함수 $C \left( \mathbf{q}, \mathbf{x}_1, \mathbf{x}_2, \mathbf{x}_3 \right) =
\left( \mathbf{q} - \mathbf{x}_1 \right) \cdot \mathbf{n} - h$는 점 $\mathbf{q}$가 천 두께 $h$만큼
삼각형 $\mathbf{x}_1, \mathbf{x}_2, \mathbf{x}_3$ 위에 있도록 합니다.
환경 충돌 (environment collision)
예를 들어 삼각형 또는 볼록 메시 (convex mesh) 로 표현되는 운동학적 모양과 입자 사이의 충돌은 먼저 각 입자에 대한 접촉면 후보의 집합을 찾아낸 다음, 각 접촉면 노멀 $\mathbf{n}$에 대해 비관통 제약을 다음과 같은 형태로 시스템에 도입하여 처리할 수 있습니다:
%%% \begin{equation} C \left( \mathbf{x} \right) = \mathbf{n}^T \mathbf{x} - d_{rest} = 0 \end{equation} %%%
여기서 $d_{rest}$는 입자가 기본적으로 지오메트리로부터 유지되어야 하는 거리입니다.
입자간 충돌 (particle collsion)
입자간 충돌은 접촉면을 선형화하고 도입하는 것으로 환경과 유사하게 처리할 수 있지만, 다음과 같은 형태로 제약의 비선형적 특성을 유지하는 것이 더 강건한 경우가 많습니다:
%%% \begin{equation} C \left( \mathbf{x}_i, \mathbf{x}_j \right) = \left| \mathbf{x}_{i,j} \right| - \left( r_i + r_j \right) \ge 0 \end{equation} %%%
여기서 $r_i$와 $r_j$는 두 입자의 반지름입니다. 이 제약은 [MMCK14]와 같이 알갱이로 구성된 재질을 모델링하는 데 사용할 수 있습니다.
마찰 (friction)
뮐러 등[MHHR07]은 제약 해결 후에 감쇠력을 도입하여 마찰을 처리했습니다. 이 접근법은 약한 마찰 효과에는 적합하지만 위치 제약이 마찰력을 자유롭게 위반할 수 있기 때문에 정적 마찰을 모델링할 수 없습니다. 제약에 비해 마찰이 강한 상황을 모델링하기 위해 (그림 9 참조), 맥클린 등[MMCK14]은 마찰 효과를 위치 레벨 제약 조건 해결의 일부로 포함시킵니다.
그림 9: 붕괴 전 모래성 (왼쪽). 300 프레임 후 위치 기반 마찰 모델은 가파른 더미를 유지하고 있는 반면 (가운데),
속도 레벨 마찰 모델은 거의 완전히 무너진 상태입니다 (오른쪽).
입자 간의 상호 침투가 해결되면, 이 타임 스텝 동안 입자의 상대적 접선 변위를 기반으로 마찰 위치 증분이 계산됩니다. 상대 변위는 다음과 같이 계산됩니다:
%%% \begin{equation} \Delta \mathbf{x}_\perp = \left[ \left( \mathbf{x}_i^* - \mathbf{x}_i \right) - \left( \mathbf{x}_j^* - \mathbf{x}_j \right) \right] \perp \mathbf{n} \end{equation} %%%
여기서 $\mathbf{x}_i^\ast$와 $\mathbf{x}_j^\ast$는 충돌하는 입자들의 이전에 적용된 제약 증분을 포함한 후보 위치를, $\mathbf{x}_i$와 $\mathbf{x}_j$는 타임 스텝의 시작점에서의 입자의 위치를, 그리고 $\mathbf{n}=\frac{\mathbf{x}_{ij}^\ast}{\left|\mathbf{x}_{ij}^\ast\right|}$는 접촉 법선 벡터입니다. 입자 $i$의 마찰 위치 증분은 다음과 같이 계산됩니다:
%%% \begin{equation} \Delta \mathbf{x}_i = \frac{w_i}{w_i + w_j} \left\{ \Delta \mathbf{x}_\perp, \left| \Delta \mathbf{x}_\perp \right| < \mu_s d, \atop \Delta \mathbf{x}_\perp \cdot \textrm{min}\left( \frac{\mu_k d}{\left| \Delta \mathbf{x}_\perp \right|}, 1 \right), \mbox{otherwise} \right. \end{equation} %%%
여기서 $d$는 침투 깊이, $\mu_k$와 $\mu_s$는 각각 동적 및 정적 마찰계수를 뜻합니다. 식 (28)의 첫번째 경우는 입자의 상대 속도가 정적 마찰력의 임계점 아래일 때 모든 접선 방향의 움직임을 제거하는 식으로 정적 마찰을 모델링합니다. 두번째 경우는 입자의 침투 깊이에 기반하여 마찰 위치 증분을 제한하는 식으로 동적 쿨롱 마찰을 모델링합니다. 입자 $j$의 위치 변화는 아래와 같이 주어집니다:
%%% \begin{equation} \Delta \mathbf{x}_j = - \frac{w_j}{w_i + w_j} \Delta \mathbf{x}_i \end{equation} %%%
운동학적 모양과의 마찰은 동일한 방법으로 처리되며, 해당 모양은 무한 질량을 가진 것으로 처리되고 접촉면은 도형의 기하적 형태에 의해 정의됩니다.
부피 보존
부피 보존은 변형 가능한 물체의 물리 시뮬레이션에서 중요한 역할을 합니다 [HJCW06, ISF07, DBB09]. 대부분의 부드러운 생체 조직은 압축되지 않기 때문에, 의료 시뮬레이션 분야에서는 필수적인 확장입니다. 하지만 부피을 보존하는 변형이 더 사실적으로 보이기 때문에 형상 모델링 분야[vFTS06]에서도 사용됩니다.
사면체 메시
사면체 메시에 대해서는 단일 사면체의 부피를 유지하는 제약을 갖는 것이 유용합니다. 이러한 제약은 다음과 같은 형태를 갖습니다:
%%% C \left( \mathbf{x}_1, \mathbf{x}_2, \mathbf{x}_3, \mathbf{x}_4 \right) = \frac{1}{6} \left( \mathbf{x}_{2,1} \times \mathbf{x}_{3,1} \right) \cdot \mathbf{x}_{4,1} - V_0 %%%
여기서 $\mathbf{x}_1, \mathbf{x}_2, \mathbf{x}_3, \mathbf{x}_4$는 사면체의 네 꼭지점이고 $V_0$은 사면체의 원래 부피입니다. 비슷한 방식으로 아래의 식을 도입하여 삼각형의 면적을 상수로 유지할 수 있습니다:
%%% C \left( \mathbf{x}_1, \mathbf{x}_2, \mathbf{x}_3 \right) = \frac{1}{2} \left| \mathbf{x}_{2,1} \times \mathbf{x}_{3,1} \right| - A_0 %%%
그림 10: 캐릭터 내부의 과압력에 대한 시뮬레이션
천 풍선 (cloth balloon)
닫힌 삼각형 메시의 경우, 그림 10과 같이 메시 내부의 과도한 압력은 메시의 모든 N개의 정점에 대한 등식 제약을 사용하여 쉽게 모델링할 수 있습니다:
%%% C \left( \mathbf{x}_1, \ldots, \mathbf{x}_N \right) = \left( \sum_{i=1}^{N_{\textrm{triangles}}} \left( \mathbf{x}_{t_1^i} \times \mathbf{x}_{t_2^i} \right) \cdot \mathbf{x}_{t_3^i} \right) - k_{\textrm{pressure}} V_0 %%%
여기서 $t_1^i, t_2^i, t_3^i$는 삼각형 $i$에 속하는 정점의 세 인덱스입니다. 위의 합은 닫힌 메시의 실제 부피를 계산합니다. 이 값은 원래 부피 $V_0$에 과압력 계수 $k_\textrm{pressure}$를 곱한 값과 비교됩니다. 이 제약 함수는 다음과 같은 그라디언트를 산출합니다.
%%% \nabla_{\mathbf{x}_i} C = \sum_{j:t_1^j=i} \left( \mathbf{x}_{t_2^j} \times \mathbf{x}_{t_3^j} \right) + \sum_{j:t_2^j=i} \left( \mathbf{x}_{t_3^j} \times \mathbf{x}_{t_1^j} \right) + \sum_{j:t_3^j=i} \left( \mathbf{x}_{t_1^j} \times \mathbf{x}_{t_2^j} \right) %%%
이 그라디언트는 식 (8)에서 주어진 스케일링 계수에 따라 스케일링하고 식 (7)에 따라 질량에 가중치를 부여하여 최종 프로젝션 오프셋 값 $\Delta \mathbf{x}_i$를 얻어야 합니다.
표면 메시 (surface meshes)
여기에서는 Diziol 등[DBB11]의 부피 보존을 위한 위치 기반 접근법을 소개합니다. 이 방법은 시뮬레이션된 물체의 표면만 고려하며 내부 입자가 필요하지 않아 계산 노력이 줄어듭니다. 부피가 있는 3D 형상 $\mathcal{V}$의 부피 $V$는 [Mir96] 및 [HJCW06]에서 제안한 발산 정리(divergence theorem)를 사용하여 결정할 수 있습니다:
%%% \begin{equation} \iiint_\mathcal{V} \nabla \cdot \mathbf{x} d\mathbf{x} = \iint_{\partial \mathcal{V}} \mathbf{x}^T \mathbf{n} d\mathbf{x} = 3V \end{equation} %%%
여기서 $\partial \mathcal{V}$는 형상의 경계면이고 $\mathbf{n}$은 표면의 법선 벡터입니다. 경계면이 삼각 메시로 주어지면 적분값은 모든 삼각형 $i$에 대한 합으로 쓸 수 있습니다:
%%% \begin{equation} V \left( \mathbf{X} \right) := \frac{1}{3} \iint_{\partial \mathcal{V}} \mathbf{x}^T \mathbf{n} d\mathbf{x} = \frac{1}{9} \sum_i A_i \left( \mathbf{x}_{i_1} + \mathbf{x}_{i_2} + \mathbf{x}_{i_3} \right)^T \mathbf{n}_i \end{equation} %%%
여기서 $A_i$는 $i$번째 삼각형의 면적을, $i_1, i_2, i_3$은 $i$번째 삼각형의 세 정점의 인덱스를 뜻합니다. 이제는 부피 제약 $C := V \left( \mathbf{X} \right) - V_0 = 0$를 정의하고 이에 상응하는 위치 보정값을 계산할 수 있습니다 (4장을 참조하세요):
%%% \begin{equation} \Delta \mathbf{x}_i^V = - \frac{ w_i C \left( \mathbf{X} \right) }{ \sum_j w_j \left\Vert \nabla_{\mathbf{x}_j} C \left( \mathbf{X} \right) \right\Vert^2 } \nabla_{\mathbf{x}_i} C \left( \mathbf{X} \right) \end{equation} %%%
가중치 $w_i$는 국지적인 부피 보존 (local volume conservation)을 실현하기 위해 사용됩니다 (아래를 참고하세요). 그라디언트는 다음과 같이 근사화할 수 있습니다:
%%% \nabla C \left( \mathbf{X} \right) \approx \frac{1}{3} \left[ \bar{\mathbf{n}}_1^T, \ldots, \bar{\mathbf{n}}_n^T \right]^T %%%
여기서 $\bar{\mathbf{n}}_i = \sum A_j \mathbf{n}_j$는 입자 $i$를 포함하는 모든 삼각형 법선을 삼각형 면적으로 가중치 합을 구한 것입니다.
식 (32)의 가중치는 다음과 같이 구해집니다:
%%% w_i = \left( 1 - \alpha \right)w_i^l + \alpha w_i^g %%%
%%% w_i^l = \frac{\left\Vert \Delta \mathbf{x}_i \right\Vert}{\sum_j \left\Vert \Delta \mathbf{x}_j \right\Vert} %%%
%%% w_i^g = \frac{1}{n} %%%
여기서 $w_i^l$과 $w_i^g$는 각각 국지적 및 전역적 부피 보존에 대한 가중치고, 사용자 정의값 $\alpha \in \left[ 0, 1 \right]$가 이 둘을 섞는데 사용됩니다. 벡터 $\Delta \mathbf{x}_i$에는 $i$번째 입자의 총 위치 변화가 담겨 있습니다. 따라서 강하게 변형된 입자들이 부피 보정에 더 많이 참여합니다. 부피 보존을 위한 위치 보정 중에 충돌 제약 조건이 위반되지 않도록 충돌하는 입자들의 가중치는 0으로 설정됩니다. 마지막으로 라플라시안 필터를 통해 가중치를 스무싱합니다.
Diziol 등은 국지적 가중치 $w_i^l$에 대한 또다른 정의를 제안합니다. 물체를 통해 부피 변화를 전파하기 위해 먼저 전처리 단계에서 지오메트리를 여러 광선으로 교차시켜 반대되는 입자의 쌍을 결정합니다. 각 입자 $i$마다 입체 반대편에 있는 입자 $k$가 하나씩 저장됩니다. 그런 다음 입자의 위치 변화 $\Delta \mathbf{x}_i$뿐만 아니라 해당 입자 쌍의 거리 변화 \Delta d_i에 따라 달라지는 국지적 가중치를 선택합니다:
%%% w_i^l = \frac{\beta s_i \Delta d_i + \left(1 - \beta \right) \left\Vert \Delta \mathbf{x}_i \right\Vert} {\sum_j \left( \beta s_j \Delta d_j + \left(1 - \beta \right) \left\Vert \Delta \mathbf{x}_j \right\Vert \right)} %%%
여기서 $s_i$는 사용자 정의 강성 파라미터이고 $\beta \in \left[0, 1 \right]$은 거리 변화의 영향력을 정의하는데 사용됩니다.
위치 보정과 유사하게 속도 보정을 수행하여 $\frac{\partial C}{\partial t}=0$이라는 제약을 충족시킵니다. 이는 divergence free velocity field를 이끌어 냅니다.
그림 11에서는 제시된 부피 보존 방법에 대한 다양한 구성을 서로 비교하고 있습니다.
그림 11: 부피 보존이 다른 네 개의 구가 판에 의해 압착되는 모습입니다. 왼쪽에서부터 오른쪽으로: 전역적 보존,
거리 제약이 있는 국지적 보존, 거리 제약이 없는 국지적 보존, 부피 보존이 없는 경우입니다.
최대 부피 손실은 각각 0.6%, 0.7%, 0.7%, 40%였습니다.
에어 메시 (air mesh)를 이용한 강건한 충돌 처리
… 계속 …
참고문헌
TODO
Comment count